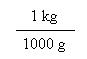
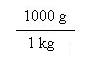
UNIT CANCELLATION - DIMENSIONAL ANALYSIS
A measurement has two parts: a number and a unit of measurement.
In science it is often necessary to express a given measurement with a different unit. To do this, you need to use a process called Unit Cancellation.
First, you will need to determine an relationship between the given unit of measurement and the desired unit of measurement. This is known as an equivalent. Some examples are:
1 kg = 1000g
1 cm = 0.01 m
1 m = 3.28 ft
Second, you will need to set up a conversion factor using the equivalent.
A conversion factor is a ratio between the two measurements of the equivalent
For example:
Using the equivalent 1 kg = 1000 g, you can make two different conversion factors. These are
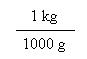
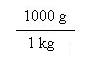
In each ratio, the measurement in the numerator equals the measurement in the denominator. Thus, each ratio is equal to 1. You can multiply anything by 1 without changing its value. So, you can multiply a given measurement by one of these ratios without changing its value. A conversion factor can be formed from any two measurements that are equal. I commonly use 5 km = 3.1 mi because I remember this relationship from Cross Country running.
Which one of the conversion factors above should you use when converting between kg and g? For any given problem, use this rule: the conversion factor is always set up so that the given unit of measurement is cancelled out when the given measurement is multiplied by the conversion factor.
Steps for Converting Between Units in Measurements
Letís convert 14.6 miles into kilometers.
1. Write the given measurement as a fraction in a "t-bar"
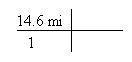
2. Write the given units in the "cross" quadrant, such that the given units will cross-cancel. The | in the t- bar means "multiply".
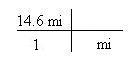
3. Write the desired units in the remaining quadrant.
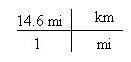
4. Now place the numbers from the equivalent in front of the appropriate units. Since 5 km = 3.1 mi
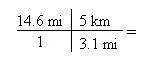
5. At this point cross-cancel the units. If you have the final units you need, stop. If not, add on more quadrants to your t-bar and repeat steps #2 thru #5.
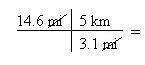
6. Now you are ready to multiply all the values in the numerators, then all the values in the denominators.
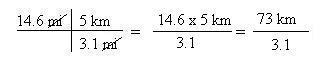
7. Next, divide the numerator by the denominator.
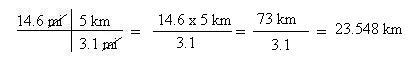
8. Finally, make sure your final answer has the same number of significant digits as your original measurement.
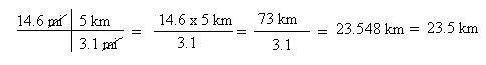
That's basically it, the rest is simply practice, practice, practice. Remember, "Practice makes permanent. You will perform what and how you have practiced."
To practice using the Unit Cancellation process for solving problems, do some basic SI conversions. You may not simply move the decimal point to the left or right any more to make SI system conversions! Why? Remember that a measurement has two parts: a number and a unit. Simply moving the decimal point for the conversion, you are changing the number part of the measurement and kind of skipping the unit part of the measurement. In science, we are dealing with measurements, and therefore we should also show the conversion of the unit as well as the number.