There are many ways to go about solving word problems. In your current, and future high school science classes the following type of process is recommended, and may even be required by some teachers. The most important aspect of this process is that when you solve a problem you should follow a process that will always lead you to a solution. When most students solve problems they try to solve it in their head after having read the problem only one time. Sorry to burst your bubble, but even the most intelligent people take the time to solve problems in ways that their solution can be verified and accepted by their peers and others that would use their solutions. It is not a sign of weakness to write down every step along the way, we all make mistakes from time to time. When you write it all down you can go back and find mistakes rather easily. If you write nothing down, and your solution is incorrect, you will probably have to re-do the entire problem. If you have it all written down you may find that you just made a calculator error, which is a quick fix. Another reason for writing down all your work is to allow others to see that your solution is valid and based upon valid principles and concepts: you didn’t just make up a solution that sounds correct.
 

The following is one simple problem solving process and is applied to a sample problem.

Sample problem:

The first step has two main parts: Read the problem and determine (1) the Knowns  and (2) the Unknown(s). The knowns are simply what you know about the situation. While most of this information is stated directly in the problem, some information is known because of the conditions stated in the problem. For example, you may have a problem dealing with an object in freefall. Even if the problem does not state the acceleration of the object it is known from the condition of freefall which accelerates objects at 9.8 m/s² near the earth’s surface. Known values may also be defined by you to simplify a problem. You are often able to define your starting time and position at zero. This may not be specifically stated in the problem, but is usually an obvious choice in many physics problems. In either case be sure that you have properly identified what you know.

The unknown(s) is that quantity(ies) which the problem is asking you to determine. It is usually directly asked for or stated in the problem. There may be multiple unknowns that you must determine before you can produce your final solution. At first this may require that you simply follow this entire process for each unknown, but as you gain experience you be able to combine the solution of multiple unknowns into fewer steps. Another useful technique in this step is to sketch the situation. Your sketch should label all the knowns and unknowns as well as indicating the appropriate direction and action of each.

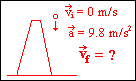
The second step is to determine an Equation that relates the unknown(s) to the knowns. Often you will not need all of the knowns to solve for your unknown(s), but you will soon discover that it is important that you have properly identified your knowns and unknown(s). Many physics problems have been solved and looked correct only to find that final velocity had been labeled as average velocity in an acceleration situation. This mistake will lead to an incorrect solution that looks correct.

The final step is where you actually Solve the problem. Here you simply substitute your knowns in to the equation and complete the algebra/arithmetic necessary to determine the value of the unknown with appropriate units and significant digits.

Although there are many ways to write out a problem solving process this is the preferred method and guideline you should use for all of your problem solving needs in Mr. Teters' classes: Knowns, Unknowns, Equation, and Solve aka K-U-E-S.